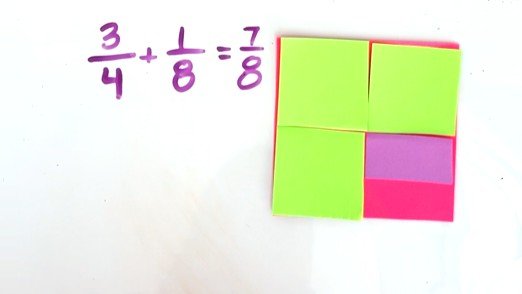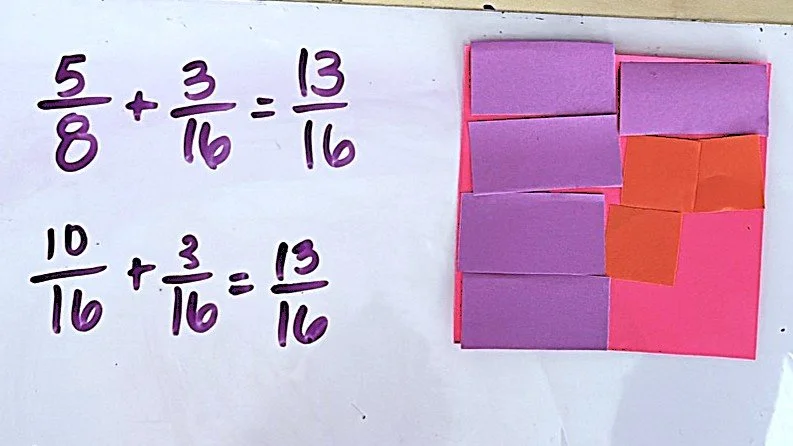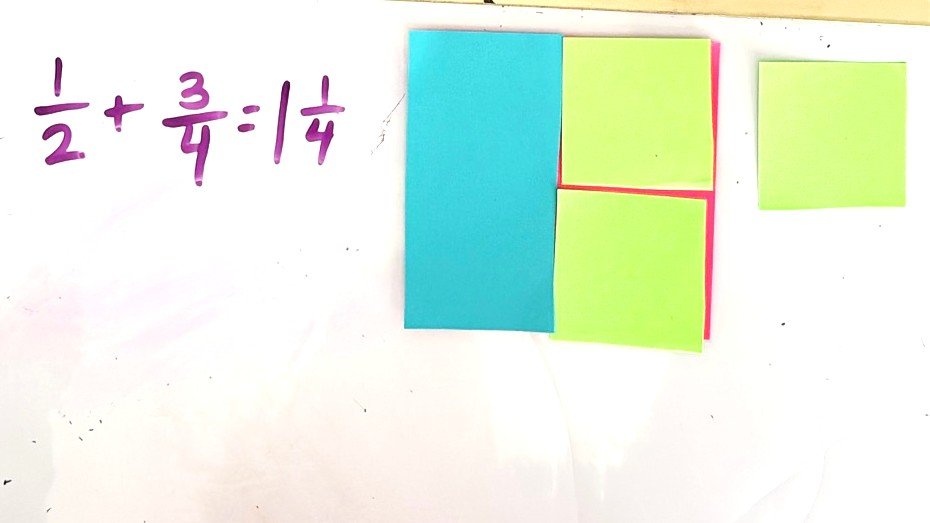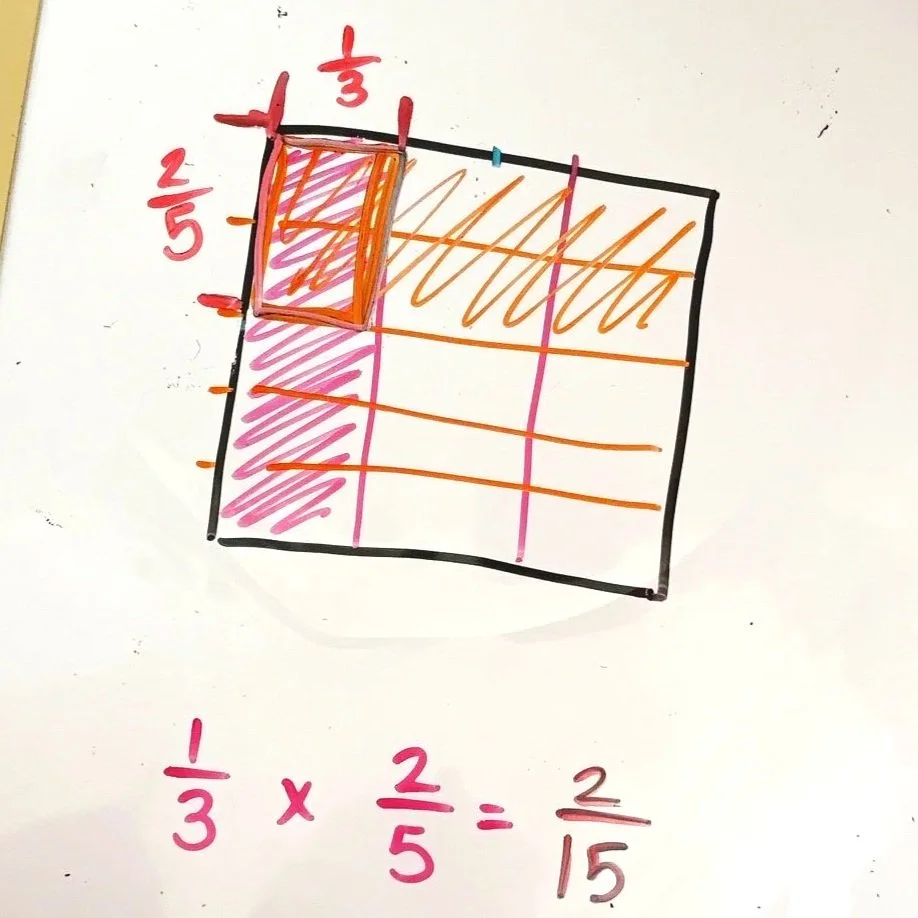Fraction Visuals that Build Understanding of Fraction Concepts

When I surveyed over two thousand math teachers asking about their students’ understanding of fractions, over 75% reported that their students either really struggled or had lots of gaps in understanding. If your students struggle with fractions, you are not alone! Fraction topics are often taught in upper elementary through 6th grade, but fraction concepts continue to affect students’ success with math through high school and beyond.

I have gathered a couple of my favorite visuals that help students really grasp the meaning of fractions and how to operate with them. These are visuals you can use whether you are teaching fractions to your students for the first time or if you are helping correct misunderstandings. Visuals help students gain a conceptual understanding of math so that it makes sense.

Paper Fraction Models

Manipulatives like fraction tiles or pattern blocks are powerful in building fraction understanding. Paper fraction models can also be a powerful tool, especially if you do not have access to manipulatives. Create paper fraction models by using 5 squares of paper, all the same size but different colors. Leave one square whole, fold and cut one into halves, one into fourths, one into eighths, and one into sixteenths as shown. Everyone in the class should cut the same color into the same pieces. (This activity is adapted from Making Sense of Mathematics for Teaching Grades 3 - 5 by Juli K. Dixon et. al.)

Equivalent Fractions

Using the paper fraction models, ask students to make observations and comparisons. The paper models will help you push their understanding and discover misconceptions.

Using the pink piece to represent one whole, we can ask what do 3 green pieces represent? What fraction is represented by 7 orange pieces? We can ask students to represent a given number (such as 1/2, 3/4, 1 1/2, 2, etc.) in as many ways as possible.

Visuals of equivalent fractions help students understand the procedures we use to create equivalent fractions. Students can pick up on patterns by comparing 1/2 and 2/4 or 6/16 and 3/8.

Then, we can really challenge them to think by changing the representation for one whole. At first, this may feel confusing (even to us), but developing a deep understanding of fractions requires understanding that the “whole” can be different in different situations. If one of the green pieces is now the whole, we can ask students what fraction does one purple piece represent? How about a pink piece? We also can challenge them by giving them a new fraction value for one piece. For example, if an orange piece is 1/8, what color piece is equal to one whole?

Adding Fractions

The paper fraction models are also helpful for modeling adding fractions with unlike denominators. In the examples, you can see how students can use the pink to represent one whole, then add the pieces to represent the fraction addends. Of course we are limited to using fractions we can represent with out pieces, but like any model, we are using this to build conceptual understanding in the early stages of learning something new. Students are using reasoning skills as they make sense of the solutions. We will challenge them to find patterns in the math that will help them to become more efficient and eventually no longer need the models.

When students begin finding sums of fractions with models and visuals, they may surprise you by finding solutions that seemingly skip steps we teach in procedures. That is a good sign! They may say they just “see” the solution. That is the goal of visuals. Seeing the solution is part of sense-making.

Having students replace pieces with equivalent amounts can help bridge using the models to using algorithms and equivalent fractions. Once students have had time to explore adding fractions with models, we can help them formalize the process into a procedure they can do without the models. However, don’t underestimate the power of using the models first! The thought process lays a solid foundation for the procedures and algorithms.

Area Models

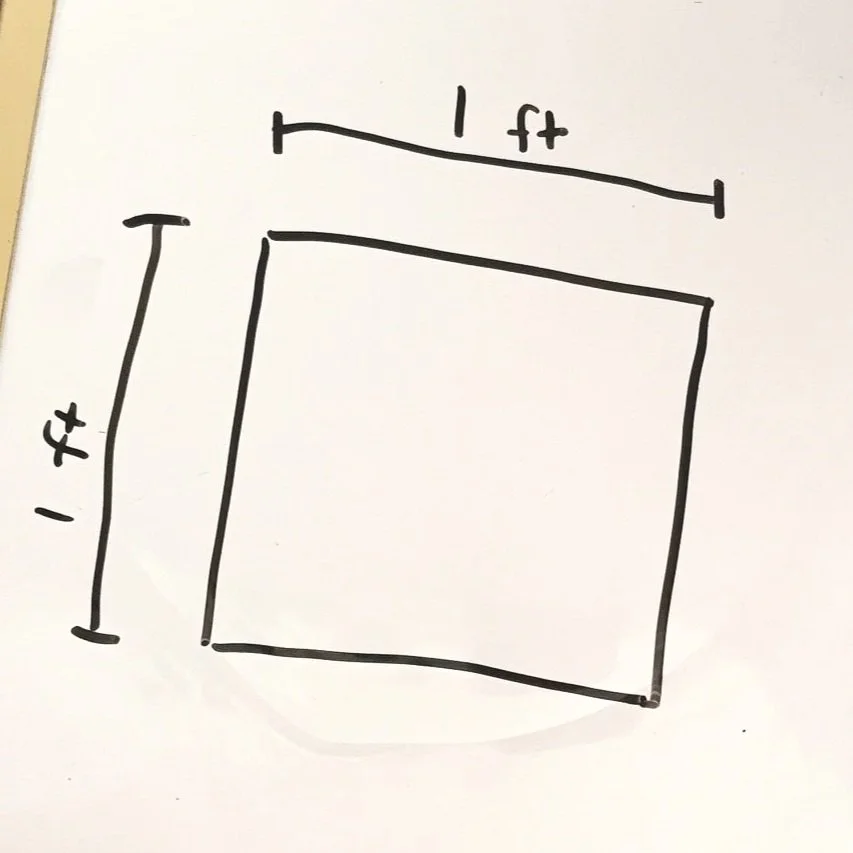
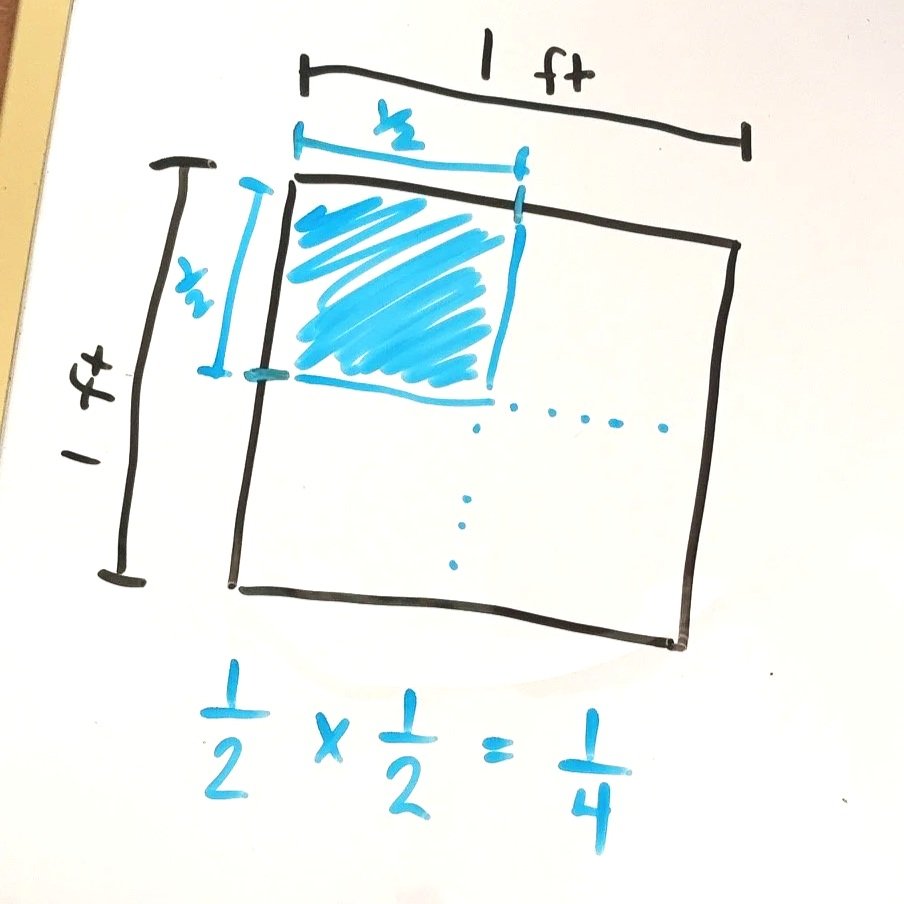
Area models are a useful tool for multiplying anything from whole numbers to decimals to polynomials. They also can help students understand fraction multiplication. However, the shading of area models to multiply fractions can feel just like a procedure for answer-getting if we are not clear on why it works. Let’s break it down and examine how area models work with fractions. We first need to back up and make sure students understand area.

Starting with a square, we’ll give it the dimensions of 1 foot by 1 foot. This square has an area of 1 square foot. Although this may seem simple, this basic understanding of how area works is crucial to really comprehending area models in a way that builds conceptual understanding.

Now if we think about multiplying 1/2 times 1/2, we can represent a square area with dimensions 1/2 by 1/2. The blue shaded portion is the area and the product. Comparing the blue square to the larger square which represents one whole, we can see the product of 1/2 x 1/2 is 1/4. Students will need exposure to several of these basic problems to help them see how an area model represents a product when we are working with fractions.

This visual shows the more common practice of shading entire rows and columns as we multiply fractions. Students create a grid, shading a horizontal row to represent one fraction and shading a vertical column to represent the other. The portion of the whole rectangle that is shaded twice is the solution. As mentioned earlier, this is a procedure that works, but students still are not always sure of the meaning behind all this shading.

As we move to these more complicated problems, context can help students make sense of the math. For example, imagine 1 cake is the size of the entire rectangle. This represent one whole cake. You have 1/3 of a cake (which you will shade pink). You cut off 2/5 of your cake piece for dessert. How much of A CAKE do you have for dessert? The wording is very important here. Our final product will represent the fraction of a whole cake. With this context, students may only shade 2/5 of the cake they have (instead of the entire row). This is acceptable and makes sense with the context.

The more models and visuals students have for fractions, the more opportunities they have to develop a strong conceptual understanding. Although it may seem confusing to show multiple models, students need it. Fractions look different in different contexts and in different problems. We need students seeing fractions represented in multiple ways. When we’re building a foundation, it’s important to focus on quality prompts and questions. Often, fewer is better. Giving students time to think, reason, and make connections will help them make sense of the math and remember it!

You might like these resources for fractions: